Packaging size optimisations
When the cutting occurs with a number of sheets equal to the packaging size, the run length should also be a multiplication of the packaging size. (e.g.: when orders have to be delivered per 84, and cutting is also done per 84 sheets, the run length should be a multiple of 84).
This influences the obtained impositions. Consider for example the following four orders you want to produce in one gang run.
| OrderID | Height | Width | Requested |
| 1 | 0.09525 | 0.05715 | 12000 |
| 2 | 0.09525 | 0.05715 | 12000 |
| 3 | 0.15875 | 0.10795 | 10000 |
| 4 | 0.22225 | 0.09525 | 5000 |
When the packaging size is set to 0, one obtains the optimal solution for the problem, whereby one wishes to produce the absolute minimum of sheets necessary.
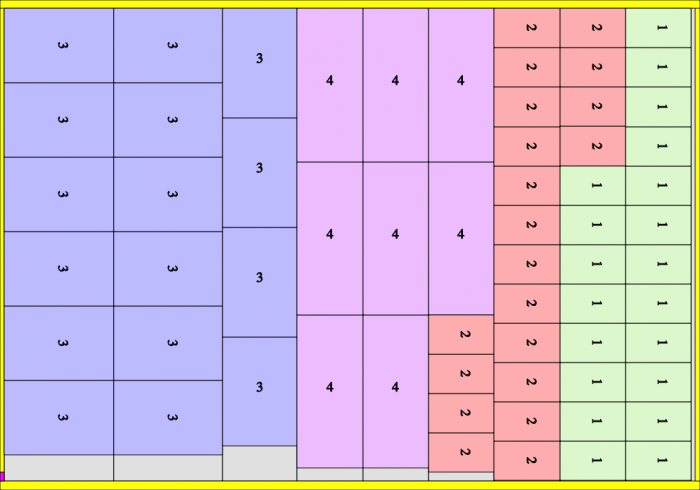
CuttingPer=0. Run length=625 sheet.
When specifying that cutting occurs per 84, one will obtain a solution that is a multiple of 84. Please notice that in this case, it is enough to place only 15 replicas of order 3 instead of 16.
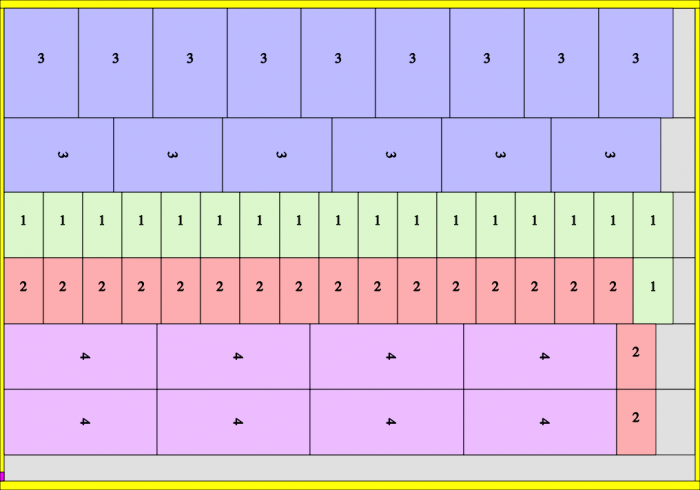
CuttingPer=84. Run length=672vel (=8*84)
When adjusting the packaging size to 128, or even further to 250, we again get a different solution.
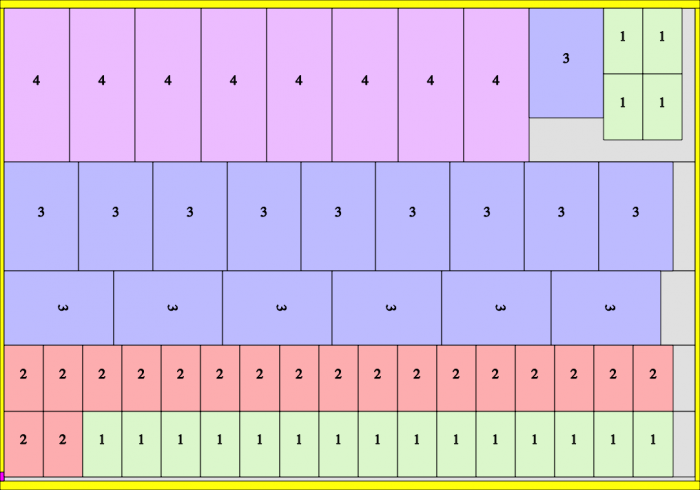
CuttingPer=128. Run length=640 drukvel (=5*128)
Changing the packaging size further to 250, again delivers another solution. Notice we again need fewer replicas than before in order to obtain the requested quantities.
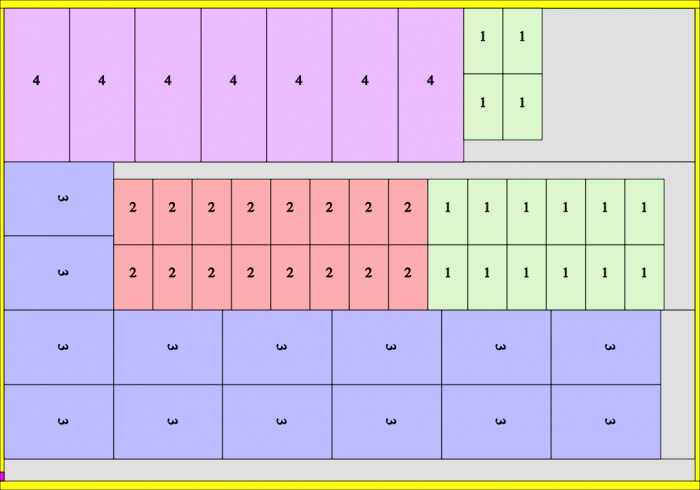
CuttingPer=250. Run length=750 sheet (=3*250)
To demonstrate the effect clearly, we will examine the solution, packaged per 500:
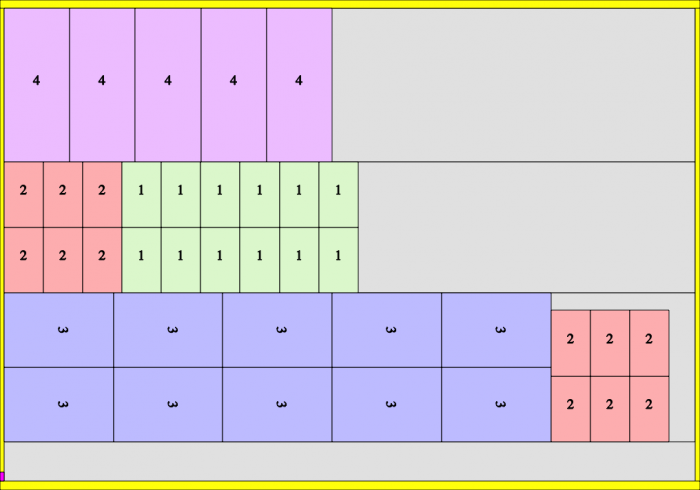
CuttingPer=500. Run length=1000 sheet (=2*500)
In this final solution, one can clearly note the empty space. This is entirely logical when one notices that the run length should be 1000 sheet, because this is the first multiple of 500 above 625 (the first solution). Also notice that for each order, a sufficient amount is produced:
| OrderID | Requested | Produced |
| 1 | 12000 | 12000 |
| 2 | 12000 | 12000 |
| 3 | 10000 | 10000 |
| 4 | 5000 | 5000 |
Indeed, it’s true that each additional replica is actually superfluous.
