Optimalisatie naar verpakkingshoeveelheid
Wanneer men snijdt in veelvouden van de verpakkingshoeveelheid, dan moet de oplage ook een veelvoud zijn van de verpakkingshoeveelheid. (vb: orders afleveren in pak per 84, als men dan ook snijdt per 84, moet de oplage een veelvoud zijn van 84).
Dit beïnvloedt de opgestelde imposities. Beschouw bijvoorbeeld volgende 4 orders die men via ganging wenst te produceren:
| OrderID | Hoogte | Breedte | Gevraagd aantal |
| 1 | 0.09525 | 0.05715 | 12000 |
| 2 | 0.09525 | 0.05715 | 12000 |
| 3 | 0.15875 | 0.10795 | 10000 |
| 4 | 0.22225 | 0.09525 | 5000 |
Wanneer men de verpakkingshoeveelheid instelt op 0, bekomt men de optimale oplossing voor het probleem, met het minimaal aantal drukvel.
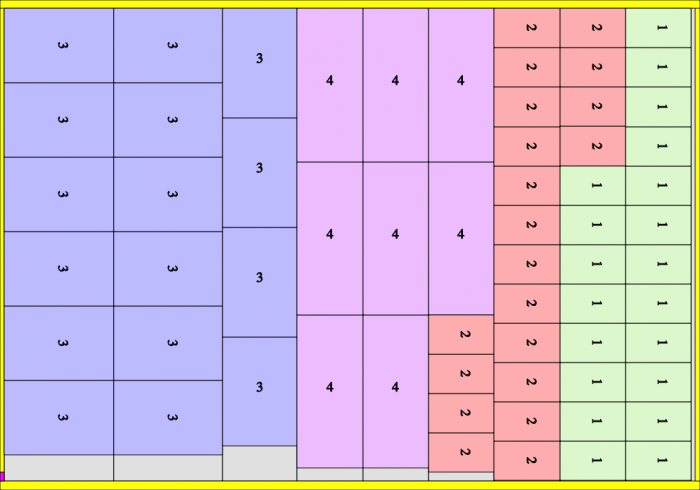
SnijdenPer=0. Oplage=625 drukvel.
Als men snijdt en verpakt per 84, dan bekomt men een oplossing waarvan de oplage een veelvoud is van 84. Merk ook op dat het dan volstaat van order 3 slechts 15 replica’s te plaatsen in plaats van 16.
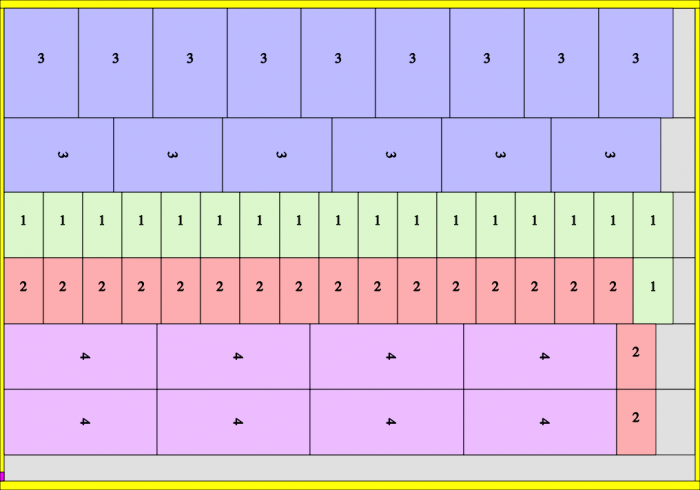
SnijdenPer=84. Oplage=672vel (=8*84)
Wijzigen we de verpakkingshoeveelheid naar 128, dan bekomen we weer een andere oplossing.
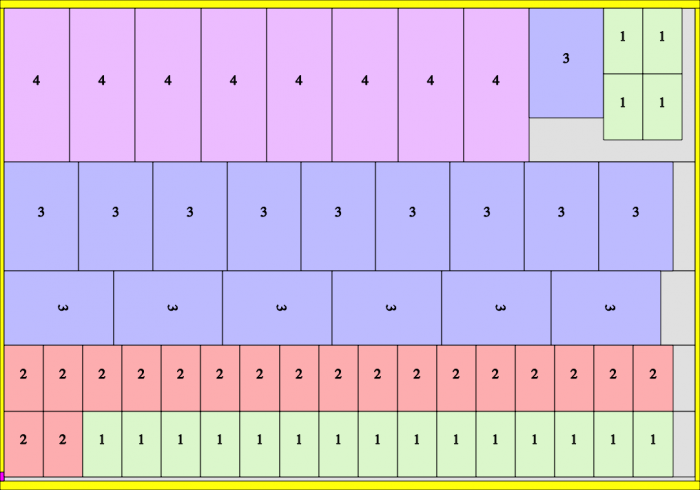
SnijdenPer=128. Oplage=640 drukvel (=5*128)
Verder verhogen naar een verpakkingshoeveelheid van 250, geeft weer een andere oplossing. Merk op dat er steeds minder replica’s nodig zijn om de gevraagde hoeveelheden te bereiken.
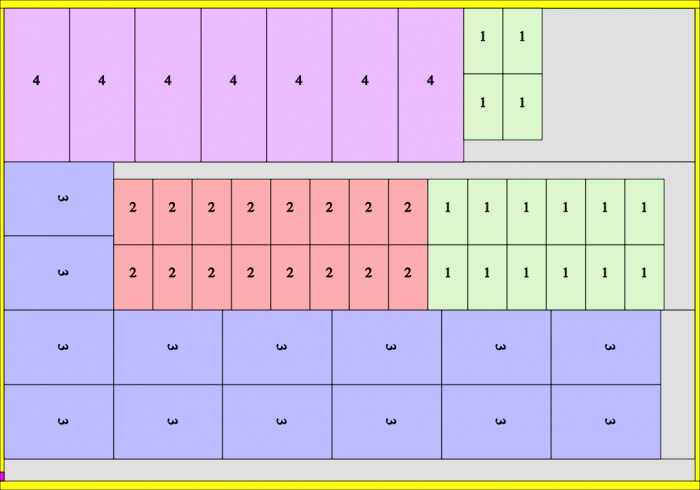
SnijdenPer=250. Oplage=750 drukvel (=3*250)
Om duidelijk te demonstreren welk effect het heeft, geven we ook nog de oplossing verpakt per 500:
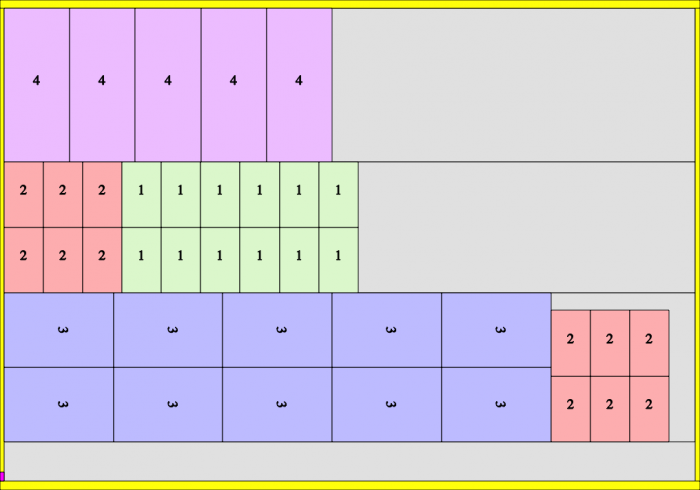
SnijdenPer=500. Oplage=1000 drukvel (=2*500)
Deze laatste oplossing valt op omdat er zoveel lege plaats is. Dit is ook logisch als men bedenkt dat de oplage 1000 drukvel moet zijn, omdat dit het eerste veelvoud is van 500 boven de 625 (eerste oplossing). Merk op dat er van elk order voldoende geproduceerd wordt:
| OrderID | Gevraagd | Geproduceerd |
| 1 | 12000 | 12000 |
| 2 | 12000 | 12000 |
| 3 | 10000 | 10000 |
| 4 | 5000 | 5000 |
Elke replica die men bijplaatst, is dus eigenlijk overbodig.
